Day 24時結尾提到幾個存在的問題：「(1) 當文集資料量變大時，每個東西出現的機率會將得非常低，所得到的最終機率也會非常低；(2) 若是有個東西出現在文集的機率為零，任何東西乘以0為0，這句話出現的機率也會因此成為0，這樣的值是沒有意義的。」

要解決這些問題，我們要介紹平滑方法。平滑方法最主要的概念就是，將過去未見過的事件也賦予一定的機率，同時還是要守住機率學最基本的假設：P(everything) = 1，所有事件之機率的總和仍舊要保持1。

有非常多種平滑方法：

• Laplacian (Add-1) smoothing
• Add-k smoothing
• Jelinek-Mercer interpolation
• Katz backoff
• Absolute discounting
• Kneser-Ney
• 還有很多其他的方法

先來介紹幾個比較容易理解的：

首先，Laplacian (Add-1) smoothing，簡稱Add-1的Laplacian smoothing最基本的想法是假裝我們把每個字都「多看了一遍」。

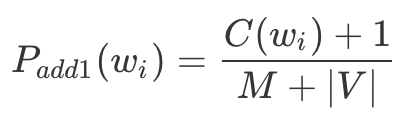
這是Unigram的Add-1公式，其中w_i是文集中能遇見的所有獨特字型、C(w_i)是這個獨特字型的次數、M是文集的總字數(所有獨特字型加總的總和)、|V|是獨特字型的數量（Vocabulary，每一個獨特字型，不論文集中有多少個該字型，那個字型都只會被算一次）。

Bigram Add-1會變成：

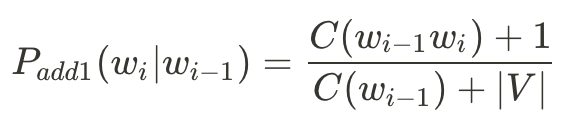
Trigram Add-1則是：

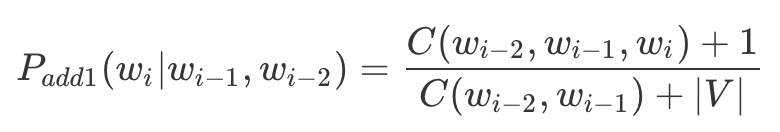
舉個例子：<s> the rat ate the cheese </s>

那麼，在bigram模型下P(ate | rat)的add-1機率會是多少呢？

首先，V = {the, rat, ate, cheese, </s>}。有注意到嗎？開頭標籤<s>沒有被列入V裡面，為什麼呢？仔細想想，<s>在這裡的用途是作為一個條件機率，只會發生P(w | <s>)的情況，而不會有P(<s> | w)的狀況，因此我們不把<s>放到V裡面來增加P_add1的分母。

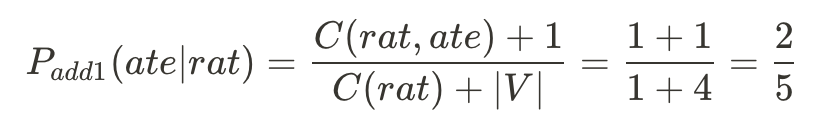
如果今天遇到沒遇過的狀況P(ate | cheese)那要怎麼辦呢？

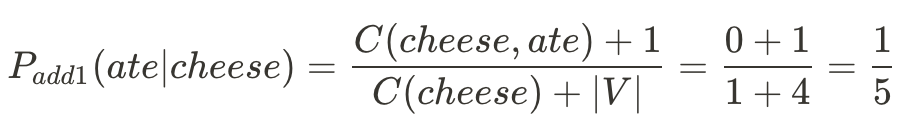
如此一來，就算是沒見過的Bigram pair也會被賦予機率。

有時候Add-1太多了，我們會用Add-k，其中k是一個分數（0 < k < 1)。

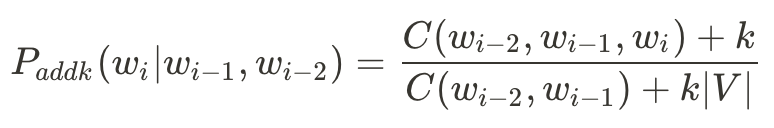
除了Add-1和Add-k，也有backoff (Katz backoff)和interpolation (Jelinek-Mercer interpolation)可以用。Backoff的概念為，每當n-gram的計次(count)為0時，我們就退一元，到(n-1)-gram去找這個條件的計次。

Interpolation則是用遞迴的概念，將相對低元的機率也一併算入

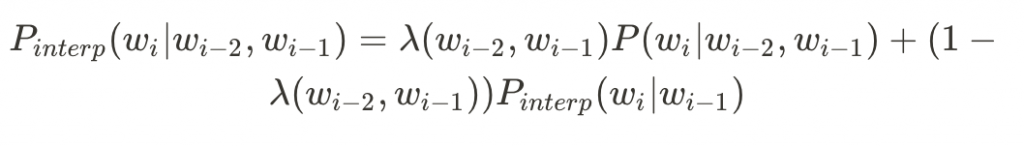
其中lambda可以透過訓練來取得，也可以用我們自己設定的常數。

而現在最常用的是Kneser-Ney Smoothing，它長得像這樣：

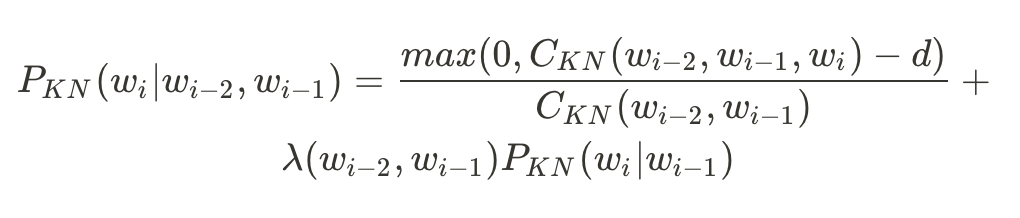
其中

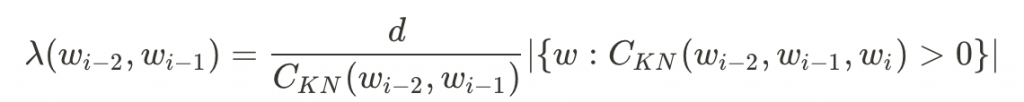
基本上KN Smoothing就是將backoff、interpolation、今天沒介紹到的absolute discounting和continuation count組合起來的一個厲害公式。